试着用计算机来解决几何问题吧(●’◡’●)

前置知识

  • 几何基础
  • 平面直角坐标系
  • 极坐标与极坐标系
  • 向量（向量积）

二维计算几何基础

图形的表示

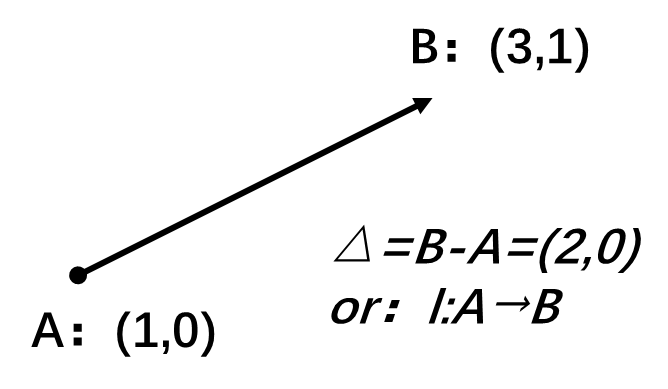
点与线的表示

例图：

image-20240312195935541 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

typedef double ld;
typedef pair<ld, ld> pld;
typedef pair<ll, ll> pll;

struct point {
    ld x, y;
    point operator+(const point& p) const {    // 加
        return { x + p.x, y + p.y };
    }
    point operator-(const point& p) const {    // 减
        return { x - p.x, y - p.y };
    }
    point operator*(const ld p) const {    // 数乘
        return { x * p, y * p };
    }
    point operator/(const ld p) const {    // 除
        return { x / p, y / p };
    }
};

struct line {
    point s, t;
};

point A(1, 0), B(3, 1), delta = B - A;
line l(A, B);

距离与旋转

例图：

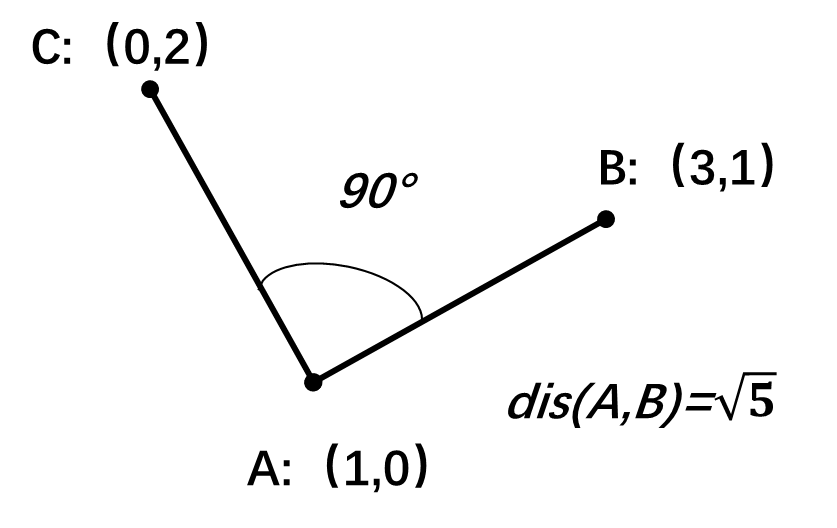
image-20240312195958430 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

ld sqr(ld x) { return x * x; }

struct point {
    ...
    point rotate(ld t)const {
        return { x * cos(t) - y * sin(t), x * sin(t) + y * cos(t) };
    }
    point rot90()const {
        return { -y,x };
    }
    point unit()const {
        return *this / sqrt(sqr(x) + sqr(y));
    }
};

ld dis(const point& a, const point& b) {
    return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));
}

point C = A + (B - A).rot90();

向量旋转解析

设$\vec{a}=(x,y)$，倾角为$\theta$，长度为$l=\sqrt{x^2+y^2}$。则$x=l\cos{\theta},y=l\sin{\theta}$，顺时针旋转后得到$\vec{b}=(l\cos{\theta+\alpha},l\sin{\theta+\alpha})$​。

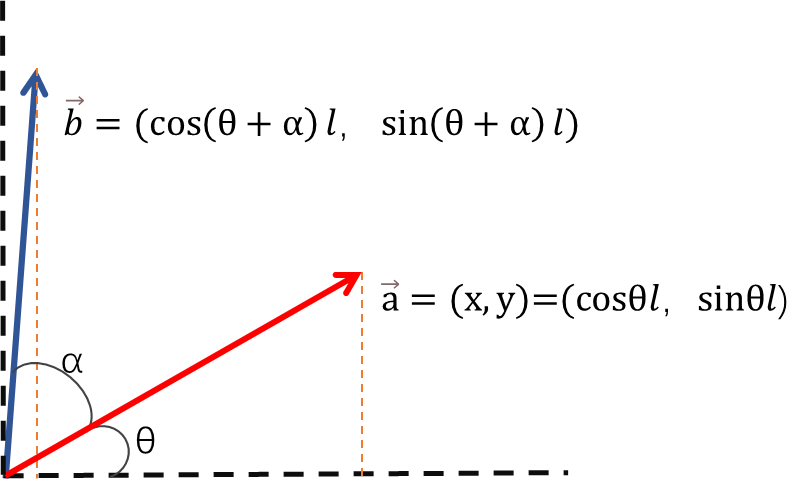
image-20240312200008353

三角恒等变化： $$ \vec{b}=(\cos{(\theta+\alpha)}l,\sin{(\theta+\alpha)}l) $$

$$ =(l(\cos{\theta}\cos{\alpha-sin{\theta}sin{\alpha}}),l(\sin{\theta}\cos{\alpha}+\sin{\alpha}\cos{\theta})) $$

$$ =(x \cos{\alpha-y \sin{\alpha},y \cos{\alpha}+x \sin{\alpha}}) $$

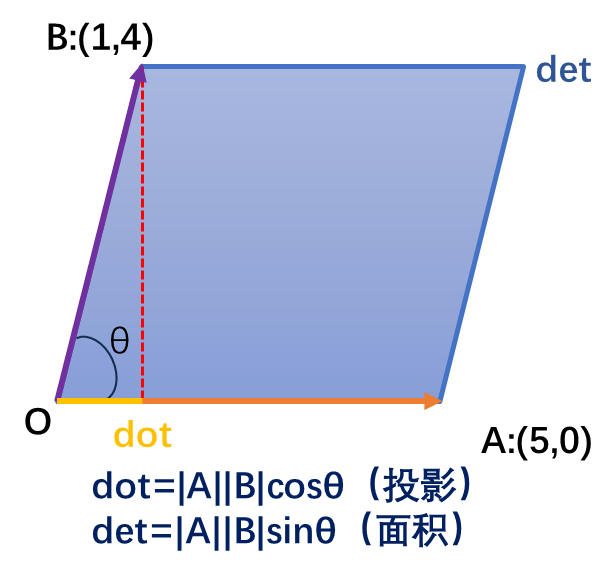
点积与叉积

例图：

image-20240312200022870 
1
2
3
4
5
6

ld dot(const point& a, const point& b) {
    return a.x * b.x + a.y * b.y;
}
ld det(const point& a, const point& b) {
    return a.x * b.y - a.y * b.x;
}
  • 点积：也叫数量积、内积。几何意义是一个向量在另一个向量上的投影再乘第二个向量的模长，是一个实数，有交换律。
    • 若同向($\theta = 0°$)，为模长之积。
    • 若锐角($\theta \lt 90°$)，数量积为正
    • 若直角($\theta = 90°$)，数量积为0
    • 若钝角($\theta \gt 90°$)，数量积为负
    • 若反向($\theta = 180°$)，为模长之积的相反数
  • 叉积：也叫外积，几何意义是两向量围成的平面四边形的面积。是一个向量，其方向$\vec{a}\times \vec{b}$：用右手从$\vec{a}$沿着不大于平角的方向向$\vec{b}$​旋转，拇指方向是外积的方向。没有交换律。
    • 若平行，外积为$\vec{0}$
    • 共起点后，对于$\vec{a}\times \vec{b}$，若$\vec{a}$在$\vec{b}$的右侧，外积为正，否则外积为负（以纸面为参考，$\vec{a}$往$\vec{b}$是逆时针为正，顺时针为负）

由向量外积可以判断两向量的旋转关系、方便求出点到直线的距离。适用于凸包和旋转卡壳。

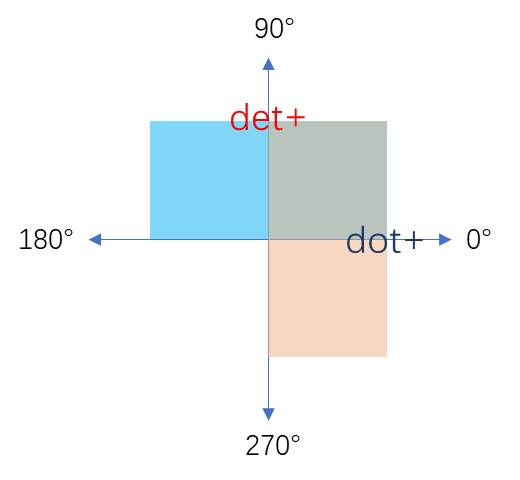
观察两个式子：

  • 投影：$dot=|A||B|\cosθ$

  • 面积：$det=|A||B|\sinθ$

可以发现点积与叉积的正负由角度决定，故根据点积和叉积的正负，可以判断向量夹角的象限。

image-20240312200034965 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

const ld eps = 1e-8;
int sgn(ld x) {
    if (fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}

bool turn_left(const point& a, const point& b, const point& c) {
    return sgn(det(b - a, c - a)) > 0;
}

bool same_dir(const line& a, const line& b) {
    return sgn(det(b.t - b.s, a.t - a.s)) == 0
        && sgn(dot(b.t - b.s, a.t - a.s)) > 0;
}

判等判交求交

浮点数等于零

注意浮点数的精度误差，一般用sgn()来实现相等判断

1
2
3
4
5

const ld eps = 1e-8;
int sgn(ld x) {
    if (fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}

点判等

也是一样要注意精度捏

1
2
3
4

friend bool operator==(const point& a, const point& b) {
    return sgn(a.x - b.x) == 0 
        && sgn(a.y - b.y) == 0;
}

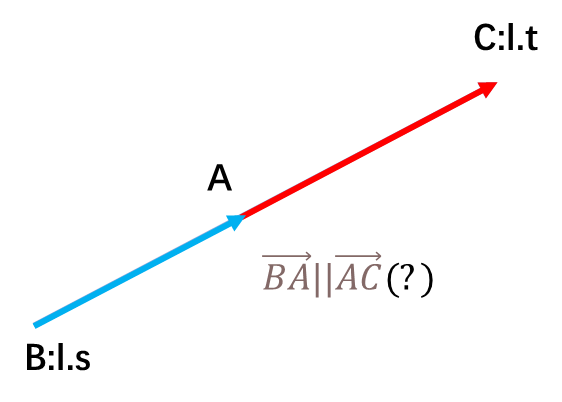
点在线段上

点在线段上有两个要求：

  • 点在直线上：叉积判断共线
  • 点在两端点上：点积判断方向

image-20240312200043778 

1
2
3
4
5

bool point_on_segment(const point& a, const line& l) {
    // 叉乘为0，点积小于0;l:BC, a:A   BA?//AC
    return sgn(det(a - l.s, l.t - a)) == 0
        && sgn(dot(a - l.s, l.t - a)) >= 0;
}
  • 叉乘为0则共线(0°或180°)

注意：可能需要处理线段退化的情况：线段退化时直接调用会返回true。

线段退化情况在调用之前自行判断。

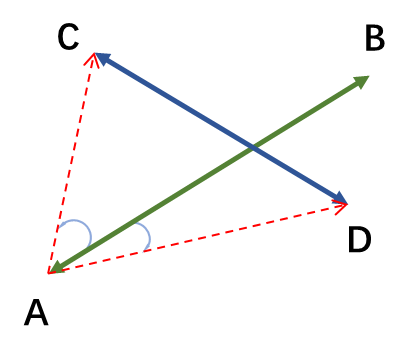
线段判交

线段有交的两种情况：

  • 一条线段的端点在另一条线段上。
  • 互相严格跨立。

第一种使用point_on_segment()处理；

第二种用叉积判断角度异号。

image-20240312200051561 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

// l:AB, c:C, d:D;ABxAC * ABxAD < 0,表明旋转方向不同(两点在线段两侧)
bool two_side(const point& c, const point& d, const line& l) {
    return sgn(det(l.t - l.s, c - l.s)) * sgn(det(l.t - l.s, d - l.s)) < 0;
}
bool inter_judge(const line& a, const line& b) {
    if (point_on_segment(a.s, b)
        || point_on_segment(a.t, b)
        || point_on_segment(b.s, a)
        || point_on_segment(b.t, a))
        return true;
    return two_side(a.s, a.t, b)
        && two_side(b.s, b.t, a);
}

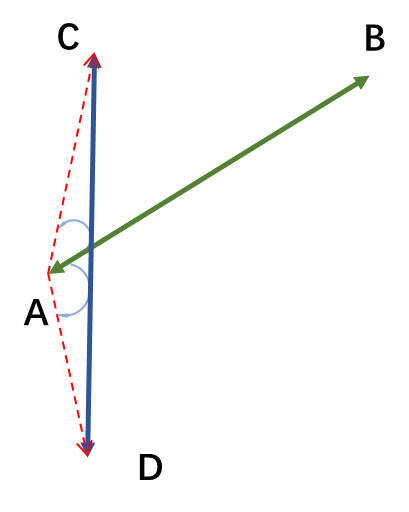
几种测试情况思考：

image-20240329151252281 image-20240329151441830
image-20240329151354763 image-20240329151611939

直线求交

求两条直线的交点

直线和直线的位置关系有三种：

  1. 平行
  2. 有一个交点
  3. 重合(共线)

判断位置关系

思路：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

if(平行) {
    if(过同一个点) {
        return 两只直线重合;
    }
    else {
        return 两直线平行;
    }
}
else {
    return 两直线相交;
}

判断平行(包括重合)：叉积是否为0

1
2
3

bool parallel_judge(const line& a, const line& b) {
    return sgn(det(a.t - a.s, b.t - b.s)) == 0
}

判断共线：平行且交换端点后也平行

1
2
3
4

bool collinear_judge(const line& a, const line& b) {
    return parallel_judge(a, b)
        && sgn(det(a.t - a.s, b.t - a.s)) == 0;
}

两直线相交求交点

使用面积计算等高三角形底边的比例求交点。

注意：这里使用了除法，除法会导致精度严重下降(通常epsilon就是为了克服除法的误差而引入的)

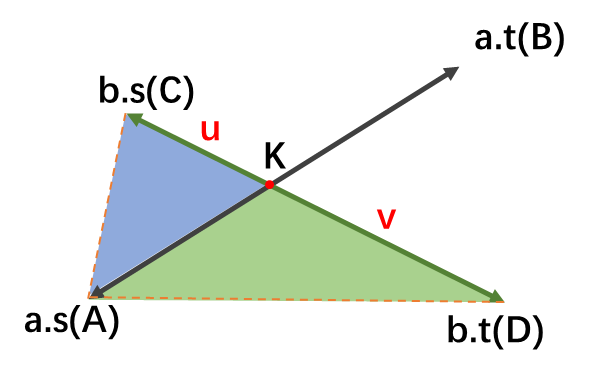
image-20240313145344069

这里$△ABC$与$△ABD$共底，面积之比（叉积之比）即为CK与KD的长度之比。则：

对$K(k_x,k_y),C(c_x,c_y),D(d_x,d_y)$，有： $$ CK=\frac{u}{u+v}CD $$ so：K是CD的一个定比分点。

1
2
3
4
5

point line_intersect(const line& a, const line& b) {
    ld u = det(a.t - a.s, b.s - a.s);
    ld v = det(a.t - a.s, b.t - a.s);
    return (b.s * v + b.t * u) / (v + u);
}

射线求交（留思考

两条射线之间的位置关系：

  1. 平行（不重合）
  2. 共线同向（部分重合或完全重合）
  3. 共线反向且不重合
  4. 共线反向且部分重合
  5. 相交

求交点

两条射线如果有相交交点的话（情况5），这个交点一定是两条射线所在直线的交点，用前文的方法求即可。

判断相交

对于射线来说，若有交点，则交点一定在两条射线所在直线上，射线可以看作其所在直线的一部分，那么只要判断这个交点是否同时在两条射线的延长线方向即可。

距离

点到线段距离

点到线短距离有两种情况：

  1. 垂线段长度
  2. 到某个端点的距离
  • 注意线段退化问题
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

ld point_to_line(const point& p, const line& l) {
    if (sgn(dis(l.s, l.t)) == 0)    // 线段退化为点
        return dis(p, l.s);
    return fabs(det(p - l.s, l.t - l.s)) / dis(l.s, l.t);
}

ld point_to_segment(const point& p, const line& l) {
    if (sgn(dot(p - l.s, l.t - l.s)) < 0)
        return dis(p, l.s);
    if (sgn(dot(p - l.t, l.s - l.t)) < 0)
        return dis(p, l.t);
    return point_to_line(p, l);
}

凸包

能包含所有给定点的最小凸多边形的叫做凸包

  • 凸多边形：每个内角在$[0,\pi)$内的简单多边形；如果允许非严格则是$[0,\pi]$
  • 或者，点集所有可能的带权平均点集合为凸包。

求凸包

有两种求法：Graham算法和Andrew算法，两种算法的时间复杂度都是$O(n\log n)$。区别在于对点的排序方式不同。

Andrew算法

对点的排序方法：按照$x$为第一关键字，$y$为第二关键字，对点集进行排序，排序完成后，易知：第1个点和第n个点一定在凸包点集里。

可以分别求出下凸壳和上凸壳，求上下两半时也不会互相影响。

算法：用栈来维护在凸包上的点

  • 逆时针先求下凸壳：第1个点和第2个先入栈，当加入更多点时，设栈中的倒数第二个点为$A$，最后一个点为$B$，新加入的点为$C$，若$B$在$\vec{AC}$的左边(或在线上)，则将$B$弹出，令$C$入栈。
  • 接下来依然是逆时针求上凸壳，上述求下凸包时，最后入栈的点一定是$n$号点，在加入$n-1$​号点后，我们继续上一步的一模一样的操作：判断旧点和新向量的位置关系再做取舍。
  • 注意，求上凸壳的时候依然是遍历到1号点，此时会有首尾相同，点重复的问题。

模版代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

vector<point>Andrew(vector<point>& p) {
    sort(p.begin(), p.end(), [](const point& a, const point& b) {
        return a.x == b.x ? a.y < b.y : a.x < b.x;
        });
    vector<point> res;
    for (int i = 0; i < p.size(); i++) {    // 下凸壳
        while (res.size() > 1 && sgn(det(res.back() - res[res.size() - 2], p[i] - res[res.size() - 2])) <= 0)
            res.pop_back();
        res.push_back(p[i]);
    }
    int k = res.size();
    for (int i = p.size() - 2; i >= 0; i--) {   // 上凸壳
        while (res.size() > k && sgn(det(res.back() - res[res.size() - 2], p[i] - res[res.size() - 2])) <= 0)
            res.pop_back();
        res.push_back(p[i]);
    }
    res.pop_back(); // 删除重复的点,即首尾相同
    return res;
}

凸包的周长：($k$为凸包中点的个数) $$ C=\sum_{i=0}^{i=k-1}dis(p_{i},p_{(i+1) \mod{k}}) $$

1
2
3
4
5
6

ld convex_perimeter(vector<point>& p) {
    ld res = 0;
    for (int i = 0; i < p.size(); i++)
        res += dis(p[i], p[(i + 1) % p.size()]);
    return res;
}

Graham算法

取左下角的点为基准，对其余点进行逆时针排序。

  • 由于其他点相对于基准点在$[0,\pi )$的半平面内，因此可以直接使用叉积排序
  • 不要使用atan2：当值域很大时，精度难以区分相近的点
  • 注意处理极角序相同的点：按照到基准点的距离从小到大排序。

用一根细线尝试绕过所有点。

  • 需要弹出不满足凸性的点
  • 使用单调栈实现
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

bool turn_left(const point& a, const point& b, const point& c) {
    return sgn(det(b - a, c - a)) > 0;
}

vector<point> Graham(vector<point>& p) {
    point base = *min_element(p.begin(), p.end(), [](const point& a, const point& b) {
        return a.y == b.y ? a.x < b.x : a.y < b.y;
        });
    sort(p.begin(), p.end(), [&](const point& u, const point& v) {
        int s = sgn(det(u - base, v - base));
        if (s)return s > 0;
        return sgn(dis(u, base) - dis(v, base)) < 0;
        });
    vector<point>res;
    for (auto i : p) {
        while (res.size() > 1
            && !turn_left(res[res.size() - 2], res.back(), i))
            res.pop_back();
        res.push_back(i);
    }
    return res;
}

两种算法相比

Graham不够好：相对较慢，容易写错

  • 相对较慢：排序需要计算$O(n\log n)$次叉积。
  • 任意写错：细节比较多，任意出现挂边界的情况。

Andrew算法扫描两遍计算出上下凸壳，通常在效率和实现上相比Graham有优势。

凸包典题：

[P2742 USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

[P3829 SHOI2012] 信用卡凸包 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

三分

二分要求单调性，最基本的应用是求一个单调函数的零点。

三分是二分的变种，它的基本用途是求单峰函数的极值点。

三分的原理：以求极大值为例。每次对一个区间$[l,r]$求三等分点$lp$和$rp$：

  • 如果$f(lp)\lt f(rp)$，说明极大值一定在$[lp,r]$内取到，因为如果在$[0,lp]$内，那$rp$一定处于单调下降的区间内，它的函数值不可能大于$f(lp)$，于是我们令$l=lp$
  • 如果$f(lp)\gt f(rp)$，同理，极大值一定在$[l,rp]$内取到，令$r=rp$

这样进行下去，直到$fabs(l-r)\lt eps$​为止，如果是求极小值，只需要把处于判断处的大于小于互换。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

ld three_section_max(ld l, ld r, function<ld(ld)> f) {
    while (r - l > eps) {
        ld m1 = l + (r - l) / 3;
        ld m2 = r - (r - l) / 3;
        if (f(m1) < f(m2)) {
            l = m1;
        }
        else {
            r = m2;
        }
    }
    return f(l);
}
// 三分求极小值
ld three_section_min(ld l, ld r, function<ld(ld)> f) {
    while (r - l > eps) {
        ld m1 = l + (r - l) / 3;
        ld m2 = r - (r - l) / 3;
        if (f(m1) > f(m2)) {
            l = m1;
        }
        else {
            r = m2;
        }
    }
    return f(l);
}

优化

按照上面的算法，每次减少三分之一的长度，但其实还可以通过在中点附近取点来优化，这样每次可以减少约二分之一的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

while (r - l > eps) {
    ld mid = (l + r) / 2;
    ld fl = f(mid - eps), fr = f(mid + eps);
    if (fl < fr) {
        r = mid;
    }
    else {
        l = mid;
    }
}

题单部分

基础

一些子问题Q

  • 如何求一组点中用一条直线穿过的最多的点数？$O(n^3)$做法、$O(n^2logm)$做法

难一些的

模版代码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double ld;
typedef pair<ld, ld> pld;
typedef pair<ll, ll> pll;
const ld eps = 1e-18;

ld sqr(ld x) { return x * x; }

int sgn(ld x) {
    if (fabs(x) < eps) return 0;
    return x < 0 ? -1 : 1;
}

struct point {
    ld x, y;

    point operator+(const point& p) const {    // 加
        return { x + p.x, y + p.y };
    }
    point operator-(const point& p) const {    // 减
        return { x - p.x, y - p.y };
    }
    point operator*(const ld p) const {    // 乘
        return { x * p, y * p };
    }
    point operator/(const ld p) const {    // 除
        return { x / p, y / p };
    }

    friend bool operator==(const point& a, const point& b) {
        return sgn(a.x - b.x) == 0
            && sgn(a.y - b.y) == 0;
    }


    point rotate(ld t)const {
        return { x * cos(t) - y * sin(t), x * sin(t) + y * cos(t) };
    }
    point rot90()const {
        return { -y,x };
    }
    point unit()const {   // 单位向量
        return *this / sqrt(sqr(x) + sqr(y));
    }
};

struct line {
    point s, t; //s起点 t终点
};

point A(1, 0), B(3, 1), delta = B - A;
line l(A, B);

ld dis(const point& a, const point& b) {
    return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));
}

point C = A + (B - A).rot90();

ld dot(const point& a, const point& b) {
    return a.x * b.x + a.y * b.y;
}
ld det(const point& a, const point& b) {
    return a.x * b.y - a.y * b.x;
}


bool turn_left(const point& a, const point& b, const point& c) {
    return sgn(det(b - a, c - a)) > 0;
}

bool same_dir(const line& a, const line& b) {
    return sgn(det(b.t - b.s, a.t - a.s)) == 0
        && sgn(dot(b.t - b.s, a.t - a.s)) > 0;
}

bool parallel(const line& a, const line& b) {
    return sgn(det(b.t - b.s, a.t - a.s)) == 0;
}

bool point_on_segment(const point& a, const line& l) {
    // 叉乘为0，点积小于0;l:BC, a:A   BA?//AC
    return sgn(det(a - l.s, l.t - a)) == 0
        && sgn(dot(a - l.s, l.t - a)) >= 0;
}

// l:AB, c:C, d:D;ABxAC * ABxAD < 0,表明旋转方向不同(两点在线段两侧)
bool two_side(const point& c, const point& d, const line& l) {
    return sgn(det(l.t - l.s, c - l.s)) * sgn(det(l.t - l.s, d - l.s)) < 0;
}
bool inter_judge(const line& a, const line& b) {
    if (point_on_segment(a.s, b)
        || point_on_segment(a.t, b)
        || point_on_segment(b.s, a)
        || point_on_segment(b.t, a))
        return true;
    return two_side(a.s, a.t, b)
        && two_side(b.s, b.t, a);
}
// 判断平行(包括重合)
bool parallel_judge(const line& a, const line& b) {
    return sgn(det(a.t - a.s, b.t - b.s)) == 0;
}
// 判断共线
bool collinear_judge(const line& a, const line& b) {
    return parallel_judge(a, b)
        && sgn(det(a.t - a.s, b.t - a.s)) == 0;
}

point line_intersect(const line& a, const line& b) {
    ld u = det(a.t - a.s, b.s - a.s);
    ld v = det(a.t - a.s, b.t - a.s);
    return (b.s * v + b.t * u) / (v + u);
}


// bool ray_intersect_judge(const line& a, const line& b) {
//     // TODO: finish this
// }

ld point_to_line(const point& p, const line& l) {
    if (sgn(dis(l.s, l.t)) == 0)    // 线段退化为点
        return dis(p, l.s);
    return abs(det(p - l.s, l.t - l.s)) / dis(l.s, l.t);
}

ld point_to_segment(const point& p, const line& l) {
    if (sgn(dot(p - l.s, l.t - l.s)) < 0)
        return dis(p, l.s);
    if (sgn(dot(p - l.t, l.s - l.t)) < 0)
        return dis(p, l.t);
    return point_to_line(p, l);
}

ld segment_to_segment(const line& a, const line& b) {
    if (inter_judge(a, b))
        return 0;
    return min({ point_to_segment(a.s, b), point_to_segment(a.t, b),
        point_to_segment(b.s, a), point_to_segment(b.t, a) });
}

vector<point>Andrew(vector<point>& p) {
    sort(p.begin(), p.end(), [](const point& a, const point& b) {
        return a.x == b.x ? a.y < b.y : a.x < b.x;
        });
    vector<point> res;
    for (int i = 0; i < p.size(); i++) {    // 下凸壳
        while (res.size() > 1
            && !turn_left(res[res.size() - 2], res.back(), p[i]))
            res.pop_back();
        res.push_back(p[i]);
    }
    int k = res.size();
    for (int i = p.size() - 2; i >= 0; i--) {   // 上凸壳
        while (res.size() > k
            && !turn_left(res[res.size() - 2], res.back(), p[i]))
            res.pop_back();
        res.push_back(p[i]);
    }
    res.pop_back(); // 删除重复的点,即首尾相同
    return res;
}

bool turn_left(const point& a, const point& b, const point& c) {
    // 逆时针
    return sgn(det(b - a, c - a)) > 0;
}

vector<point> Graham(vector<point>& p) {
    point base = *min_element(p.begin(), p.end(), [](const point& a, const point& b) {
        return a.y == b.y ? a.x < b.x : a.y < b.y;
        });
    sort(p.begin(), p.end(), [&](const point& u, const point& v) {
        int s = sgn(det(u - base, v - base));
        if (s)return s > 0;
        return sgn(dis(u, base) - dis(v, base)) < 0;
        });
    vector<point>res;
    for (auto i : p) {
        while (res.size() > 1
            && !turn_left(res[res.size() - 2], res.back(), i))
            res.pop_back();
        res.push_back(i);
    }
    return res;
}

// 求凸包的周长
ld convex_perimeter(vector<point>& p) {
    ld res = 0;
    for (int i = 0; i < p.size(); i++)
        res += dis(p[i], p[(i + 1) % p.size()]);
    return res;
}



void solve() {}

int main() {
    solve();

    return 0;
}