2025牛客暑寒假多校训练营Day3（完結）

DODOLA 收录于类别在学算法的日子里和系列题解记录

2025-02-16 2025-03-18 约 9028 字预计阅读 19 分钟次阅读

https://img.dodolalorc.cn/i/2025/02/16/67b17bacd70e1.jpg

系列 - 题解记录

A 智乃的博弈游戏

题意

有一堆$n$个石子，每次可以拿走$x$个石子，要求$x$是一个不大于$n$且与$n$互质的数，当面对$1$时选手获胜，询问智乃（先手玩家）能否获胜。

数据范围

$1\leq n\leq 1e18$

思路

必胜点是剩余 1，则 2 是必败点，两个选手都不希望对手面对 1，都希望对手面对 2。

如果当前剩余$n$是奇数，则选手一定可以操作将剩余数量变成偶数（只拿一个）。面对偶数的选手，能选的互质的数一定是一个奇数，偶数减去奇数会变成奇数，下一轮回到奇数的情况，如果某一方保持偶数，一定会到剩余$2$的情况，也就是必败点。

于是本题博弈和初始状态的奇偶性相关。

代码

1
2
3
4
5
n = int(input())
if n & 1:
    print("Yes")
else:
    print("No")

B 智乃的质数手串

题意

有一个环形的手串，第一个小球的编号是$0$，上面有一个数字$a_0$…第$n$个小球的编号是$n-1$，上面有一个数字$a_{n-1}$。

遵循以下规则：

手串上只有一个小球，则可以直接取下。
若当前小球上的数字和其顺时针相邻的下一个小球的数字相加的和是一个质数，则可以拿下当前的小球。

给出手串的结构，请问是否可以将小球全部取下来，取下来的合法序号顺序是什么？

数据范围

$1\leq n\leq 1e5$
$1\leq a_i\leq 1e5$

思路

当手串是链状的时候，若要将第一个取下来，则需要将序号大于 1 的第一个小球前的所有小球取下来，或者第二个小球前的所有小球取下来…很明显这是一个栈的结构，当将要入栈的小球可以和栈顶的数构成质数，则进行pop操作，知道栈为空或不能构成质数，才停止操作，将小球入栈。

而在环状手串上，需要维护一个长度为$n$的区间，在这个区间上测试是否存在栈的大小只剩 1 的情况，当栈底的小球的序号与栈顶的序号超过$n$的区间长度，需要将栈底的pop，这个数据结构需要支持两端的pop操作，应当使用deque模拟操作。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>

using namespace std;

typedef double ld;
typedef unsigned long ul;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll> pll;

const ll maxn = 2e6 + 50;

ll lowbit(ll x) { return x & -x; }

ll a[maxn], b[maxn], c[maxn], d[maxn];
ll pre[maxn], suf[maxn];
ll diff[maxn];
bool vis[maxn];

vector<ll> primes;
bool isprime[maxn];
void init_prime() {
  ll w = maxn - 1;
  for (ll i = 0; i <= w; i++) {
    isprime[i] = true;
  }
  isprime[0] = isprime[1] = false;
  for (ll i = 2; i <= w; i++) {
    if (!isprime[i])
      continue;
    for (ll j = 2 * i; j <= w; j += i) {
      isprime[j] = false;
    }
  }
}
vector<vector<ll>> factors;
void init_factor() {
  ll w = maxn - 1;
  factors.assign(w + 1, vector<ll>());
  for (ll i = 1; i <= w; i++) {
    for (ll j = i; j <= w; j += i) {
      factors[j].push_back(i);
    }
  }
}

void solve() {
  ll n;
  cin >> n;
  for (ll i = 0; i < n; i++) {
    cin >> a[i];
    a[i + n] = a[i];
  }
  deque<pll> q;
  ll pos = -1;
  for (ll i = 0; i < 2 * n; i++) {
    while (!q.empty() && isprime[a[i] + q.back().first]) {
      q.pop_back();
    }
    while (!q.empty() && i - q.front().second + 1 > n) {
      q.pop_front();
    }
    q.push_back({a[i], i});
    if (q.size() == 1 && i >= n) {
      pos = i % n; // 最后一个入栈的数
      break;
    }
  }

  if (pos == -1) {
    cout << "No\n";
    return;
  }
  cout << "Yes\n";
  q.clear();
  for (ll i = pos + 1; i <= pos + n; i++) {
    while (!q.empty() && isprime[a[i] + q.back().first]) {
      cout << q.back().second << ' ';
      q.pop_back();
    }
    q.push_back({a[i], i % n});
  }
  cout << q.back().second << '\n';
}

void init() { init_prime(); }

int main(void) {
  ios::sync_with_stdio(false);
  cin.tie(0);
  ll _t = 1;
  init();
  while (_t--) {
    solve();
  }

  return 0;
}

C 智乃的 Notepad(Easy version)

题意

有$n$个字符串，需要将它们都单独呈现在显示屏上，只能使用$26$个字母和退格键(\b可以删去一个字符)，提问至少需要敲几下键盘？

数据范围

$1\leq n\leq 1e5$
$m=1$
$\sum|s_i|\leq 1e6$

思路

当两个单词前缀相同时，对比分别打印两个单词，可以减少一个公共前缀的长度的次数，最后可以把最长的单词留在屏幕上。

若建立字典树，答案就是字典树上边的数量的两倍减去最长单词的长度。

也可以根据字典序排序，也可以把前缀相同的放在相邻的位置。

代码：字典序排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void solve() {
  ll n, m;
  cin >> n >> m;
  ll mx = 0;
  vector<string> v;
  for (ll i = 1; i <= n; i++) {
    string s;
    cin >> s;
    v.push_back(s);
    mx = max((ll)s.size(), mx);
  }
  sort(v.begin(), v.end());
  while (m--) {
    ll l, r;
    cin >> l >> r;
    ll ans = v[0].size() * 2;
    for (ll i = 1; i < n; i++) {
      ll j = 0;
      ans += v[i].size() * 2;
      while (j < (ll)v[i - 1].size() && j < (ll)v[i].size() &&
             v[i - 1][j] == v[i][j]) {
        j++;
      }
      ans -= j * 2;
    }
    cout << ans - mx << '\n';
  }
}

代码：字典树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
ll tot = 0;
ll tree[maxn][26];
bool exist[maxn];
void insert(string s, ll n) {
  ll p = 0;
  for (ll i = 0; i < n; i++) {
    ll c = s[i] - 'a';
    if (!tree[p][c]) {
      tree[p][c] = ++tot;
    }
    p = tree[p][c];
  }
  exist[p] = true;
}

void solve() {
  ll n, m;
  cin >> n >> m;
  ll mx = 0;
  for (ll i = 1; i <= n; i++) {
    string s;
    cin >> s;
    insert(s, s.size());
    mx = max((ll)s.size(), mx);
  }
  while (m--) {
    ll l, r;
    cin >> l >> r;
    ll ans = tot * 2 - mx;
    cout << ans << '\n';
  }
}

D 智乃的 Notepad(Hard version)

题意

情景同 C 题，在此版本，需要支持$m$次查询，得到完成打印区间$[l,r]$内的单词需要的最少操作次数。

数据范围

$1\leq n\leq 1e5$
$1\leq m\leq 1e5$
$\sum|s_i|\leq 1e6$

思路

离线处理查询的区间，范围$[l,r]$内的操作数是以$[l,r]$内的单词建立的字典树的边数 ×2-最长单词长度，考虑字典树的建树过程，每个单词会覆盖前若干个单词的部分前缀，在覆盖的过程中，前面的单词的贡献的点数部分转移到当前的单词上，将字符串的序号看作不同的颜色，在着色的过程中，更新各个颜色对应的贡献，在加入新的单词$i$时，可以计算所有以$i$为右端点的查询区间的答案。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
ll lowbit(ll x) { return (x) & (-x); }

ll n, m;
ll a[maxn], b[maxn], c[maxn];

ll bitree[maxn];          // BIT树
void update(ll p, ll x) { // 单点修改a[p]+=x
  while (p && p <= n) {
    bitree[p] += x;
    p += lowbit(p);
  }
}
ll query(ll n) {
  ll ans = 0, p = n;
  while (p) {
    ans += bitree[p];
    p -= lowbit(p);
  }
  return ans;
}
ll query(ll l, ll r) { return query(r) - query(l - 1); }

ll tot = 0;
ll tree[maxn][26], clr[maxn];
void insert(string s, ll t) {
  ll n = s.size();
  s = " " + s;
  ll p = 0;
  for (ll i = 1; i <= n; i++) {
    ll c = s[i] - 'a';
    if (!tree[p][c]) {
      tree[p][c] = ++tot;
    }
    p = tree[p][c];
    if (clr[p]) {
      update(clr[p], -1);
    }
    clr[p] = t; // 当前颜色
    update(clr[p], 1);
  }
}

// ST表
ll dp[maxn][50]; // 0/1:最小值/最大值
void rmq_st(ll n, vector<ll> &v) {
  for (ll i = 1; i <= n; i++) {
    dp[i][0] = v[i]; // 2^0
  }
  ll m = log(1 * n) / log(2.0);
  for (ll j = 1; j <= m; j++) {
    ll t = n - (1 << j) + 1;
    for (ll i = 1; i <= t; i++) {
      dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);
    }
  }
}
ll rmq_query(ll l, ll r) { // 从l开始,长度为r的区间最大值
  ll k = log(1.0 * (r - l + 1)) / log(2.0);
  ll mx = max(dp[l][k], dp[r - (1 << k) + 1][k]);
  return mx;
}

void solve() {
  cin >> n >> m;

  vector<string> s(n + 1);
  vector<ll> sz(n + 1);

  for (ll i = 1; i <= n; i++) {
    cin >> s[i];
    sz[i] = s[i].size();
  }
  rmq_st(n, sz);

  vector<array<ll, 3>> v;
  for (ll i = 1; i <= m; i++) {
    ll l, r;
    cin >> l >> r;
    v.push_back({r, l, i});
  }
  sort(v.begin(), v.end());

  ll cr = 0;
  for (auto [r, l, i] : v) {
    while (cr < r) {
      cr++;
      insert(s[cr], cr);
    }
    a[i] = 2 * query(l, r) - rmq_query(l, r);
  }
  for (ll i = 1; i <= m; i++) {
    cout << a[i] << '\n';
  }
}

E 智乃的小球

题意

在水平线上有$n$个小球，每个小球有一个初始速度，记向右为正，小球的初始速度要么为$1m/s$，要么为$-1m/s$，其质量都相同，坐标为$p_i$。询问在足够长的时间内，能否发生$k$次碰撞，以及第$k$次碰撞发生的时间。

数据范围

$1\leq n\leq 1e5$
$1\leq k\leq 1e9$
$0\leq p_i\leq 1e9,v_i\in {-1,1}$

保证一开始所有的小球位置不同。

思路

根据高中物理常识，易得，当两个质量相同的小球相向碰撞，会交换彼此的速度。由于本题中所有小球的速度都是$1m/s$或$-1m/s$，可以把交换速度看作两个小球互相穿过对方，依然按照原来的速度向前运动。

也就是说，本题询问若干向右的小球和向左的小球能相遇多少次，这个值可以枚举某个方向的小球的初始位置，再在另一个方向的小球中二分查找当前的小球会遇到多少相向的小球，再对时间进行二分。

第$k$次碰撞的时刻的值大概率是浮点数，在二分时间的时候注意精度不要太小，容易超时。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
void solve() {
  ll n, k;
  cin >> n >> k;
  vector<ld> v1, v2;
  for (ll i = 1; i <= n; i++) {
    ll p, v;
    cin >> p >> v;
    if (v == 1)
      v1.push_back(p);
    else
      v2.push_back(p);
  }
  sort(v1.begin(), v1.end()), sort(v2.begin(), v2.end());
  // k可行性
  ll mk = 0;
  for (ll pi : v1) {
    mk += v2.end() - upper_bound(v2.begin(), v2.end(), pi);
  }
  if (k > mk) {
    cout << "No\n";
    return;
  }

  auto check = [&](ld t) {
    // 这段时间内的碰撞次数
    ll tot = 0;
    t /= 1e7;
    for (ll pi : v1) {
      ll t1 = v2.end() - lower_bound(v2.begin(), v2.end(), pi);
      ll t2 = v2.end() - lower_bound(v2.begin(), v2.end(), pi + 2 * t);
      ll ti = t1 - t2;
      tot += ti;
    }
    return tot;
  };
  ll l = 0, r = 1e16;
  while (l + 1 < r) { // [l,r]
    ll mid = (l + r) / 2;
    if (check(mid) >= k) {
      r = mid;
    } else {
      l = mid;
    }
  }
  cout << "Yes\n";
  cout << fixed << setprecision(9) << 1.0 * l / 1e7 << '\n';
}

F 智乃的捉迷藏

题意

在三角形的三个角和三条边着 6 个位置分别设计放多少人，人数总和是$n$，让 A、B、C 三个人分别能看到 a、b、c 数量的人。

数据范围

$1\leq n\leq 20$
$1\leq a,b,c\leq n$

思路

赛时是直接冲了 6 重循环，暴力 for 遍历枚举 6 个位置的数量可以通过此题（注意边界）。

也可以仅枚举 3 个顶点的位置，计算三边位置的值，判断成立条件。

代码：枚举 6 位

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
void solve() {
  ll n, a, b, c;
  cin >> n >> a >> b >> c;
  bool flag = false;
  for (ll i = 0; i <= n; i++) {
    for (ll j = 0; j + i <= n; j++) {
      for (ll k = 0; k + j + i <= n; k++) {
        for (ll x = 0; x + k + j + i <= n; x++) {
          for (ll y = 0; y + x + k + j + i <= n; y++) {
            ll z = n - (y + x + k + j + i);
            if (x + y + z == a && z + i + j == b && x + k + j == c) {
              flag = true;
              break;
            }
          }
          if (flag)
            break;
        }
        if (flag)
          break;
      }
      if (flag)
        break;
    }
    if (flag)
      break;
  }
  if (flag) {
    cout << "Yes\n";

  } else {
    cout << "No\n";
  }
}

代码：枚举 3 位

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
void solve() {
  ll n, a, b, c;
  cin >> n >> a >> b >> c;
  for (ll i = 0; i <= n; i++) {
    for (ll j = 0; i + j <= n; j++) {
      for (ll k = 0; i + j + k <= n; k++) {
        // 枚举1 3 5号位置
        ll x = a - i - j, y = b - j - k, z = c - i - k;
        if (x >= 0 && y >= 0 && z >= 0 && (i + j + k + x + y + z == n)) {
          cout << "Yes\n";
          return;
        }
      }
    }
  }
  cout << "No\n";
}

G 智乃与模数

题意

对一个正整数$n$，选择所有$1\leq i\leq n$的$i$作为模数，记录余数序列，再将余数序列降序排列，求前$k$大的数之和。

数据范围

$1\leq k\leq n\leq 1e9$

思路

分块，枚举商，在商比较小的时候，商是连续有值的，当商比较大的时候，可能会出现商和商之间不再连续，如$n=5$时，商为$1$的有${5,4,3}$，商为$2$的有${2}$，商为$3,4$的集合都是空的，商为$5$的集合是${1}$，对每个商相同的集合，可以发现其余数符合等差数列的规律，公差是商的值。商不连续的情况的数值范围比较小，可以通过打表记录这部分的余数。

二分找出第$k$大的余数的值，再在每个按商分块的集合中，利用等差数列公式，计算余数大于等于$k$的余数之和，再减去多算的数量（这部分多算的数都是余数数值为$k$的数）。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
void solve() {
  ll n, k;
  cin >> n >> k;

  vector<pll> v;
  vector<ll> w;
  for (ll i = 1; i <= n; i++) {
    if (n / (n / i) == i) {
      ll l = n / (i + 1) + 1, r = n / i;
      v.push_back({l, r});
    } else {
      v.push_back({1, n / i});
      for (ll j = 1; j <= n / i; j++) { // 打表商不连续的部分
        w.push_back(n % j);
      }
      break;
    }
  }
  sort(w.begin(), w.end());

  ll ans = 0ll, cnt = 0ll;
  auto check = [&](ll x) {
    // 统计有多少大于等于k的
    ll ret = 0ll;
    ans = 0ll;
    for (auto &[l, r] : v) {
      ll s = n / r, t = (r - l + 1);
      if (n / l != s) {
        for (auto p = lower_bound(w.begin(), w.end(), x); p != w.end(); p++) {
          ret++;
          ans += *p;
        }
        break;
      }
      ll at = n % l, a1 = n % r, d = s;
      if (x <= a1) {
        ll j = t;
        ret += j, ans += (at + a1) * j / 2;
        continue;
      }
      ll ti = (x - a1) / d + 2 - ((x - a1) % d == 0);
      ll j = max(0ll, t - ti + 1);
      ret += j, ans += (at + a1 + (t - j) * d) * j / 2;
    }
    cnt = ret;
    return ret;
  };
  ll l = 0, r = n;
  while (l + 1 < r) {
    ll mid = (l + r) / 2;
    if (check(mid) >= k) {
      l = mid;
    } else {
      r = mid;
    }
  }
  ans -= (cnt - k) * l;
  cout << ans << '\n';
}

类似题：因数个数和

H 智乃与黑白树

题意

一棵节点数为$n$的黑白树，每个节点为黑色或白色，定义一棵黑白树的权值是树中所有黑色节点到白色节点的简单路径长度之和，路径长度是路径中经过边的数量。

询问如果切掉第$i$条边，产生的两棵子树的权值分别是多少？

数据范围

$2\leq n\leq 1e5$

思路

换根更新以$i$为根的子树的权值。

flowchart TB
c1((p))-.连接.->a1((v))
subgraph 子树v
a1-->a2((s1))
a1-->a3((s2))
end
subgraph 当前的树p
c1-->c2((s1))
c1-->c3((s2))
end

如图，当前的操作是将子树$v$的信息更新到以$p$为根的树上，记以$i$为根的子树的黑/白色节点数是$num[i][0/1]$，子树$i$中的黑/白色节点到根$i$的距离之和是$g[i][0/1]$，$f[i]$为子树$i$的权值，那么在 dfs 递归更新的时候，转移是：

1
2
3
4
5
6
7
void pushup(ll rt, ll p) { // 更新以rt为根，p为子节点的信息
  f[rt] += f[p] + g[rt][0] * num[p][1] + g[rt][1] * num[p][0] +
           (num[p][0] + g[p][0]) * num[rt][1] +
           (num[p][1] + g[p][1]) * num[rt][0];
  g[rt][0] += num[p][0] + g[p][0], g[rt][1] += num[p][1] + g[p][1];
  num[rt][0] += num[p][0], num[rt][1] += num[p][1];
}

而删边的时候转移是反过来：

1
2
3
4
5
6
7
void cutlink(ll rt, ll p) { // 切断rt为父节点的子树p
  g[rt][0] -= num[p][0] + g[p][0], g[rt][1] -= num[p][1] + g[p][1];
  num[rt][0] -= num[p][0], num[rt][1] -= num[p][1];
  f[rt] -= f[p] + g[rt][0] * num[p][1] + g[rt][1] * num[p][0] +
           (num[p][0] + g[p][0]) * num[rt][1] +
           (num[p][1] + g[p][1]) * num[rt][0];
}

在切边的时候，按顺序换根，更新权值。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
ll f[maxn], g[maxn][2], num[maxn][2], clr[maxn];
ll fa[maxn];
vector<vector<ll>> tree;
void add_edge(ll u, ll v) {
  tree[u].push_back(v);
  tree[v].push_back(u);
}

void pushup(ll rt, ll p) { // 更新以rt为根，p为子节点的信息
  f[rt] += f[p] + g[rt][0] * num[p][1] + g[rt][1] * num[p][0] +
           (num[p][0] + g[p][0]) * num[rt][1] +
           (num[p][1] + g[p][1]) * num[rt][0];
  g[rt][0] += num[p][0] + g[p][0], g[rt][1] += num[p][1] + g[p][1];
  num[rt][0] += num[p][0], num[rt][1] += num[p][1];
}
void cutlink(ll rt, ll p) { // 切断rt为父节点的子树p
  g[rt][0] -= num[p][0] + g[p][0], g[rt][1] -= num[p][1] + g[p][1];
  num[rt][0] -= num[p][0], num[rt][1] -= num[p][1];
  f[rt] -= f[p] + g[rt][0] * num[p][1] + g[rt][1] * num[p][0] +
           (num[p][0] + g[p][0]) * num[rt][1] +
           (num[p][1] + g[p][1]) * num[rt][0];
}

void dfs(ll p, ll fr) {
  fa[p] = fr;
  num[p][clr[p]]++;
  for (auto v : tree[p]) {
    if (v == fr)
      continue;
    dfs(v, p);
    pushup(p, v);
  }
}

void solve() {
  ll n;
  string s;
  cin >> n >> s;
  s = " " + s;
  for (ll i = 1; i <= n; i++) {
    clr[i] = s[i] == 'w';
  }
  tree.assign(n + 1, vector<ll>());
  vector<pll> ve;
  for (ll i = 1; i <= n - 1; i++) {
    ll u, v;
    cin >> u >> v;
    add_edge(u, v);
    ve.push_back({u, v});
  }
  ll cur = 1; // 当前根节点
  dfs(cur, -1);
  for (auto [u, v] : ve) {
    ll p;
    if (fa[v] == u)
      p = v;
    else
      p = u;
    vector<pll> w;
    while (p != cur) {
      w.push_back({fa[p], p}); // 要切除的边
      p = fa[p];
    }
    reverse(w.begin(), w.end());
    for (ll k = 0; k < (ll)w.size(); k++) {
      auto [i, j] = w[k];
      // 将i<-j变成j->i
      cutlink(i, j);
      if (k == (ll)w.size() - 1)
        cout << f[u] << ' ' << f[v] << '\n';
      pushup(j, i);
      fa[i] = j;
      cur = j;
    }
  }
}

类似提：树学

I 智乃的兔子跳

题意

在坐标${x_1,x_2,\dots ,x_n}$上各有一个胡萝卜，这$n$个胡萝卜的坐标各不重合，兔子要选择一个起始坐标$p$和一个跳跃步长$k$，以获得最多的胡萝卜个数。求出获得最多胡萝卜的$p$和$k$。

数据范围

$1\leq n\leq 1e5$
$1\leq x_i\leq 1e9$
$0\leq p\leq 1e9$
$2\leq k\leq 1e9$

思路

随机化算法，如果每个坐标上都有胡萝卜，设计步长为 2，可以获得$\max (奇数个数,偶数个数)$个胡萝卜，任选两个胡萝卜，在最佳方案中的概率会大于$\frac{1}{2}\times \frac{1}{2}$，随机选择两个胡萝卜，枚举其距离的质因数，更新最优的方案，随机的次数不超过可行的时间复杂度即可。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
void solve() {
  ll n;
  cin >> n;
  for (ll i = 1; i <= n; i++) {
    cin >> a[i];
  }

  if (n == 1) {
    cout << a[1] << " 2\n";
    return;
  }

  ll ans = 0, pi = a[1], ki = 2;
  auto update = [&](ll p, ll k) {
    ll cnt = 0;
    for (ll i = 1; i <= n; i++) {
      if ((a[i] - p) % k == 0)
        cnt++;
    }
    if (cnt > ans) {
      ans = cnt;
      pi = p, ki = k;
    }
  };

  auto check = [&](ll x, ll y) {
    x = a[x], y = a[y];
    ll d = abs(y - x);
    ll k = d;
    ll p = x % k;
    for (ll t = 2; t * t <= d; t++) {
      if (d % t == 0) {
        while (d % t == 0)
          d /= t;
        k = t;
        p = x % k;
        update(p, k);
      }
    }

    if (d > 1) {
      k = d;
      p = x % k;
      update(p, k);
    }
  };

  random_device rd;
  mt19937 gen(rd());
  uniform_int_distribution<> rnd(1, n);

  ll tot = 100;
  while (tot--) {
    ll i = rnd(gen);
    ll j = rnd(gen);
    while (i == j) {
      j = rnd(gen);
    }
    if (abs(a[i] - a[j]) <= 1)
      continue;
    check(i, j);
  }

  cout << pi << ' ' << ki << '\n';
}

J 智乃画二叉树

题意

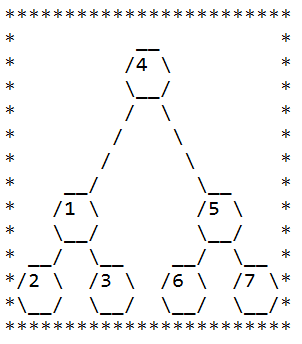
使用\、/、_画六边形二叉树，形似：

https://img.dodolalorc.cn/i/2025/02/25/67bd4123237d5.png

要去掉不存在的节点，并用一圈*区分范围。

数据范围

$1\leq n\leq 99$
$1\leq k\leq 7$

思路

先画出满二叉树，再根据树的结构填写序号和删去节点。

代码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
ll a[maxn], b[maxn];
ll fa[maxn];

ll tot;
pll tree[400];

ll w(ll i) {
  if (i == 1)
    return 4;
  return (w(i - 1) + 1) << 1;
}
ll h(ll i) { return 3 * (1ll << (i - 1)); }

ll H, W;

char maz[200][400];
void paint() { // 满二叉树
  memset(maz, ' ', sizeof(maz));
  vector<pll> v;
  for (ll j = 0; j < 3; j++) {
    for (ll i = 1; i <= W; i++) {
      char c = ' ';
      if ((j == 0 && i % 6 == 1) || (j == 1 && i % 6 == 4) ||
          (j == 2 && i % 12 == 7)) {
        c = '\\';
      } else if ((j == 0 && i % 6 == 4) || (j == 1 && i % 6 == 1) ||
                 (j == 2 && i % 12 == 4)) {
        c = '/';
      } else if ((j == 0 || j == 2) && (i % 6 == 2 || i % 6 == 3)) {
        c = '_';
      } else if (j == 1 && i % 6 == 2) {
        c = '0';
      }
      maz[H - j][i] = c;
      if (j == 2 && (i % 12 == 4 || i % 12 == 7)) {
        v.push_back({H - j, i});
      }
    }
  }

  while (v.size() >= 2) {
    while (v.size() >= 2 && v[1].second - v[0].second > 3) { // 延长线
      vector<pll> tmp;
      for (ll i = 0; i < (ll)v.size(); i++) {
        pll p = v[i];
        char c = maz[p.first][p.second];
        if (i % 2 == 0)
          p.first -= 1, p.second += 1;
        else
          p.first -= 1, p.second -= 1;
        maz[p.first][p.second] = c;
        tmp.push_back(p);
      }
      v = tmp;
    }

    vector<pll> tmp;

    for (ll i = 0; i + 1 < (ll)v.size(); i += 2) {
      pll p = v[i];
      p.first -= 1;
      maz[p.first][p.second] = '\\', maz[p.first][p.second + 1] = '_',
      maz[p.first][p.second + 2] = '_', maz[p.first][p.second + 3] = '/',
      p.first -= 1;
      maz[p.first][p.second] = '/', maz[p.first][p.second + 1] = '0',
      maz[p.first][p.second + 3] = '\\';
      p.first -= 1;
      maz[p.first][p.second + 1] = maz[p.first][p.second + 2] = '_';
      if (i % 4 == 0) {
        p.second += 3;
        maz[p.first][p.second] = '/';
        tmp.push_back(p);
      } else {
        maz[p.first][p.second] = '\\';
        tmp.push_back(p);
      }
    }
    v = tmp;
  }

  maz[v.front().first][v.front().second] = ' ';

  tot = 1;
  for (ll i = 1; i <= H; i++) {
    for (ll j = 1; j <= W; j++) {
      if (maz[i][j] == '0') {
        tree[tot++] = {i, j};
      }
    }
  }
}

void dfs(ll p, ll i) {
  if (p < 10)
    maz[tree[i].first][tree[i].second] = p + '0';
  else
    maz[tree[i].first][tree[i].second] = p / 10 + '0',
    maz[tree[i].first][tree[i].second + 1] = p % 10 + '0';

  if (a[p] != -1)
    dfs(a[p], i * 2);
  if (b[p] != -1)
    dfs(b[p], i * 2 + 1);
}
ll nI, I, nJ, J;
void cut_zero() {
  for (ll i = 1; i < tot; i++) {
    pll p = tree[i];
    if (maz[p.first][p.second] != '0') {
      I = max(I, p.first + 1);
      J = max(J, p.second + 2);
      nI = min(nI, p.first - 1);
      nJ = min(nJ, p.second - 1);
      continue;
    }
    // 删掉六边形
    maz[p.first][p.second] = maz[p.first][p.second - 1] =
        maz[p.first][p.second + 2] = ' ';
    maz[p.first + 1][p.second - 1] = maz[p.first + 1][p.second] =
        maz[p.first + 1][p.second + 1] = maz[p.first + 1][p.second + 2] = ' ';
    maz[p.first - 1][p.second] = maz[p.first - 1][p.second + 1] = ' ';
    // 删掉延长线
    char c = maz[p.first - 1][p.second - 1];
    if (c == ' ') {
      c = maz[p.first - 1][p.second + 2];
      p.first -= 1, p.second += 2;
    } else {
      p.first -= 1, p.second -= 1;
    }
    while (c != ' ' && maz[p.first][p.second] == c) {
      maz[p.first][p.second] = ' ';
      if (c == '/')
        p.first -= 1, p.second += 1;
      else
        p.first -= 1, p.second -= 1;
    }
  }
}

void solve() {
  ll n, k;
  cin >> n >> k;
  for (ll i = 1; i <= n; i++) {
    fa[i] = -1;
  }
  H = h(k), W = w(k);
  paint();
  for (ll i = 1; i <= n; i++) {
    cin >> a[i] >> b[i];
    if (a[i] != -1)
      fa[a[i]] = i;
    if (b[i] != -1)
      fa[b[i]] = i;
  }
  ll rt = -1;
  for (ll i = 1; i <= n; i++) {
    if (fa[i] == -1) {
      rt = i;
      break;
    }
  }
  // 填数
  dfs(rt, 1);
  // 删
  nI = H, nJ = W, I = 1, J = 1;
  cut_zero();
  // 打印
  for (ll i = nI - 1; i <= I + 1; i++) {
    for (ll j = nJ - 1; j <= J + 1; j++) {
      if (i == nI - 1 || i == I + 1 || j == nJ - 1 || j == J + 1) {
        cout << '*';
      } else {
        cout << maz[i][j];
      }
    }
    cout << '\n';
  }
}

K 智乃的逆序数

题意

定义一个紧密排序数组：将数组元素按照从小到大排序后，相邻元素之间的差值是$1$。当两个数组没有任何相同元素，则这两个数组是不相交的。

现在有$n$个互不相交的紧密数组，用这些数组中的元素组合成一个逆序数恰好为$k$的新数组，要求新数组中的数之间保持各自在原来数组中的相对顺序。

数据范围

$1\leq n\leq 1000$
$0\leq k\leq 1e6$
$1\leq a_{i,j}\leq 1e9$
测试文件的数组长度之和不超过$10^3$

思路

新数组中不改变数字之间在原数组中的相对顺序，且这些数组不会相交，那么每个数组是一个范围在$[l,r]$的数的排列，不管怎么改变他们在新数组中的位置，这个小排列中的数形成的逆序数对对数不会减少或增加，当按照最小值排序依次填入新数组时，就是逆序数最小的新数组。

数组之间按照最小值为第一关键字升序排序，如果排序序号较大的数组中的元素放在序号小的数组中的数前面，会增加逆序数。最多的逆序数是数组按照逆序填入新数组时，从大到小枚举数组，计算元素需要向前移动几个位置能恰好满足$k$，也可以按组进行冒泡排序，合法的冒泡排序交换的次数就是增加的逆序数的数量。

代码：枚举

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
pair<vector<ll>, ll> inverse_num(vector<ll> v) {  // 归并排序求逆序数
  ll n = v.size();
  if (n <= 1)
    return {v, 0};
  ll mid = n / 2;
  vector<ll> vl, vr;
  for (ll i = 0; i < n; i++) {
    if (i < mid)
      vl.push_back(v[i]);
    else
      vr.push_back(v[i]);
  }
  auto [arr_l, invl] = inverse_num(vl);
  auto [arr_r, invr] = inverse_num(vr);
  ll nl = arr_l.size(), nr = arr_r.size();

  arr_l.push_back(inf), arr_r.push_back(inf);

  ll i = 0, j = 0;

  vector<ll> arr;
  ll inv = invl + invr;
  while (i < nl || j < nr) {
    if (arr_l[i] <= arr_r[j]) {
      inv += j;
      arr.push_back(arr_l[i]);
      i++;
    } else {
      arr.push_back(arr_r[j]);
      j++;
    }
  }
  return {arr, inv};
}

void solve() {
  ll n, k;
  cin >> n >> k;

  vector<vector<ll>> v;
  vector<array<ll, 3>> info;

  ll tot_len = 0;
  ll min_ans = 0, max_ans = 0;
  for (ll i = 0; i < n; i++) {
    ll m;
    cin >> m;
    tot_len += m;
    vector<ll> w(m);
    for (auto &j : w) {
      cin >> j;
    }
    v.push_back(w);
    ll ni = inverse_num(w).second;
    info.push_back({*min_element(w.begin(), w.end()), m, i});
    min_ans += ni, max_ans += ni;
  }

  // 每个数组的最小元素，大小，位置
  sort(info.begin(), info.end());
  for (ll i = 0; i < n; i++) {
    auto [l, m, idx] = info[i];
    if (i == 0) {
      pre[i] = m;
    } else {
      pre[i] = pre[i - 1] + m;
    }
  }
  for (ll i = n - 1; i >= 0; i--) {
    auto [l, m, idx] = info[i];
    max_ans += (pre[i] - m) * m;
  }
  if (k < min_ans || k > max_ans) {
    cout << "No\n";
    return;
  }

  cout << "Yes\n";
  ll ans = min_ans, i = n - 1, p = 0;
  ll las = -1;
  vector<ll> arr(tot_len, -1);
  while (ans < k && i < n && i >= 0) {
    auto [l, m, idx] = info[i];
    auto w = v[idx];
    if (ans + (pre[i] - m) * m <= k) {
      // 数组idx放在首位
      for (ll j = p; j <= p + m - 1; j++) {
        arr[j] = w[j - p];
      }
      p += m;
      ans += (pre[i] - m) * m;
      i--;
      continue;
    }

    ll t = (k - ans) / (pre[i] - m); // 完整挪动t个数
    for (ll j = p; j <= p + t - 1; j++) {
      arr[j] = w[j - p];
    }
    p += t;
    ll ti = (pre[i] - m) * (t + 1) - (k - ans);
    arr[p + ti] = w[t];
    las = t + 1;
    break;
  }
  for (ll j = 0; j < i; j++) {
    auto [l, m, idx] = info[j];
    for (auto e : v[idx]) {
      while (arr[p] != -1 && p + 1 < tot_len)
        p++;
      arr[p++] = e;
    }
  }
  for (ll j = las == -1 ? 0 : las; i < n && i >= 0 && j < info[i][1]; j++) {
    auto [l, m, idx] = info[i];
    ll e = v[idx][j];
    while (arr[p] != -1 && p + 1 < tot_len)
      p++;
    arr[p++] = e;
  }

  for (auto i : arr) {
    cout << i << ' ';
  }
  cout << '\n';
}

代码：冒泡排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
void solve() {
  ll n, k;
  cin >> n >> k;

  vector<vector<ll>> v;
  vector<array<ll, 3>> info;

  ll min_ans = 0, tot = 0;
  for (ll i = 0; i < n; i++) {
    ll m, l = inf;
    cin >> m;
    tot += m;
    vector<ll> w(m);
    for (auto &j : w) {
      cin >> j;
      l = min(l, j);
    }
    v.push_back(w);
    ll ni = 0;
    for (ll t = 0; t < m; t++) {
      for (ll f = t + 1; f < m; f++) {
        ni += (w[t] > w[f]);
      }
    }
    min_ans += ni;
    info.push_back({l, m, i});
  }

  if (k < min_ans) {
    cout << "No\n";
    return;
  }

  // 进行一定次数的冒泡排序
  sort(info.begin(), info.end());
  k -= min_ans;

  vector<pll> arr;

  for (ll i = 0; i < n; i++) {
    ll idx = info[i][2];
    for (ll j : v[idx]) {
      arr.push_back({j, idx});
    }
  }

  for (ll i = 0; i < tot && k > 0; i++) {
    for (ll j = 0; j < tot - 1; j++) {
      if (arr[j].first < arr[j + 1].first &&
          arr[j].second != arr[j + 1].second && k > 0) {
        k--;
        swap(arr[j], arr[j + 1]);
      } else if (k <= 0) {
        break;
      }
    }
  }

  if (k > 0) {
    cout << "No\n";
    return;
  }

  cout << "Yes\n";
  for (auto i : arr) {
    cout << i.first << ' ';
  }
  cout << '\n';
}

L 智乃的三角遍历

题意

由三角形构成的平面图，给出层数，找出一条遍历所有边的欧拉回路。

https://img.dodolalorc.cn/i/2025/02/16/67b13c49a710b.png

数据范围

思路

$n$比较小，可以打表存答案输出。

法 2：要找出一种可以在任意层数上复刻的遍历思路，下图是一种思路，每次先向下遍历连到下层的点，再回复到右端点。

https://img.dodolalorc.cn/i/2025/02/16/67b13c2ae3c4b.png

法 3：递归搜索，类比汉诺塔，如果想完成 1→2→3→1 的顺序，需要先把以 2 为上顶点的三角形遍历完，指针回复到 2 号位置，继续完成 2→3，遍历 3 为上顶点的三角形，最后回到 1。

代码：某种顺序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
void solve() {
  ll n;
  cin >> n;
  vector<ll> v;
  ll p = 1;
  v.push_back(p);
  for (ll i = 1; i <= n; i++) {
    p += i;
    v.push_back(p);
  }
  while (p + 1 < 1 + (n + 1 + 1) * (n + 1) / 2) {
    p++;
    v.push_back(p);
  }
  for (ll x = n + 1; x >= 2; x--) {
    p -= x;
    ll pi = p;
    v.push_back(p);
    while (p > 1 + (x - 2) * (x - 1) / 2) {
      v.push_back(p + x - 1);
      p--;
      v.push_back(p);
    }
    while (p + 1 <= pi) {
      p++;
      v.push_back(p);
    }
  }
  cout<<"Yes\n";
  for (auto i : v) {
    cout << i << ' ';
  }
  cout << "\n";
}

代码：递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
vector<ll> ans;
vector<vector<pll>> G;
ll tot;
void add_edge(ll p1, ll p2) {
  vis[tot] = false;
  G[p1].push_back({p2, tot}); // 终点和这条边的编号
  G[p2].push_back({p1, tot++});
}

void dfs(ll p) {
  for (auto i : G[p]) {
    if (vis[i.second])
      continue;
    vis[i.second] = true;
    dfs(i.first);
  }
  ans.push_back(p);
}

void solve() {
  ll n;
  cin >> n;
  G.assign((n + 1) * (n + 2) / 2 + 1, vector<pll>());
  for (ll i = 1; i <= n; i++) {
    // 第i层
    for (ll j = 1; j <= i; j++) {
      ll p1 = (i - 1) * i / 2 + j;
      ll p2 = p1 + i, p3 = p1 + i + 1;
      add_edge(p1, p2);
      add_edge(p2, p3);
      add_edge(p3, p1);
    }
  }
  dfs(1);
  cout << "Yes\n";
  for (auto i : ans) {
    cout << i << ' ';
  }
  cout << '\n';
}

M 智乃的牛题

题意

判断输入的长度为 8 的字符串能不能重组字符顺序组成nowcoder。

数据范围

无

思路

无

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
void solve() {
  string s;
  cin >> s;
  map<char, ll> mp;
  for (auto c : s) {
    mp[c]++;
  }
  if (mp['n'] == 1 && mp['o'] == 2 && mp['w'] == 1 && mp['c'] == 1 &&
      mp['d'] == 1 && mp['e'] == 1 && mp['r'] == 1) {
    cout << "happy new year\n";
  } else {
    cout << "I AK IOI\n";
  }
}

目录

2025牛客暑寒假多校训练营Day3（完結）

A 智乃的博弈游戏

题意

数据范围

思路

代码

B 智乃的质数手串

题意

数据范围

思路

代码

C 智乃的 Notepad(Easy version)

题意

数据范围

思路

代码：字典序排序

代码：字典树

D 智乃的 Notepad(Hard version)

题意

数据范围

思路

代码

E 智乃的小球

题意

数据范围

思路

代码

F 智乃的捉迷藏

题意

数据范围

思路

代码：枚举 6 位

代码：枚举 3 位

G 智乃与模数

题意

数据范围

思路

代码

H 智乃与黑白树

题意

数据范围

思路

代码

I 智乃的兔子跳

题意

数据范围

思路

代码

J 智乃画二叉树

题意

数据范围

思路

代码

K 智乃的逆序数

题意

数据范围

思路

代码：枚举

代码：冒泡排序

L 智乃的三角遍历

题意

数据范围

思路

代码：某种顺序

代码：递归

M 智乃的牛题

题意

数据范围

思路

代码

相关内容

2025牛客暑寒假多校训练营Day4

2025牛客暑寒假多校训练营Day2

2025牛客暑寒假多校训练营Day1（完結）