线性动态规划,即具有线性阶段划分的动态规划。
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
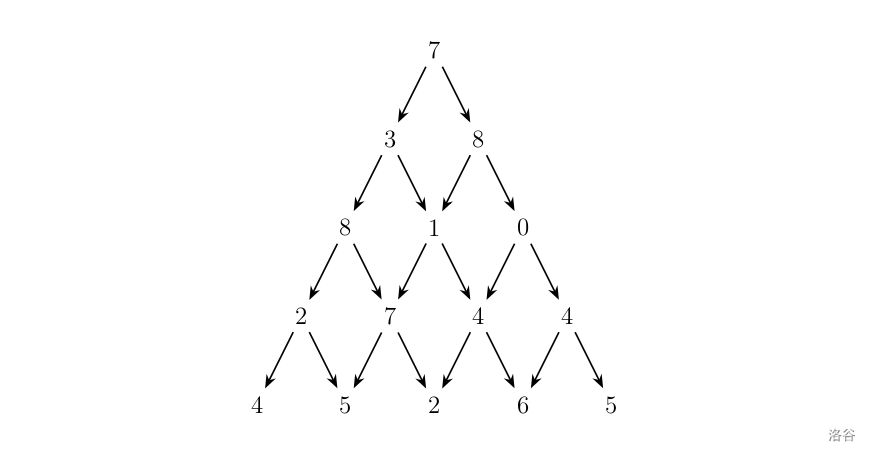
在上面的样例中,从 $7 \to 3 \to 8 \to 7 \to 5$ 的路径产生了最大权值。
输入格式
第一个行一个正整数 $r$ ,表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式
单独的一行,包含那个可能得到的最大的和。
样例 #1
样例输入 #1
1
2
3
4
5
6
| 5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
|
样例输出 #1
提示
【数据范围】
对于 $100%$ 的数据,$1\le r \le 1000$,所有输入在 $[0,100]$ 范围内。
题目翻译来自NOCOW。
USACO Training Section 1.5
IOI1994 Day1T1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 120;
ll number[maxn][maxn];
ll dp[maxn][maxn]; // 记录走到(i,j)点时最好的和
int main() {
int n;
cin >> n;
for (int i = 1;i <= n;i++)
for (int j = 1;j <= i;j++)
cin >> number[i][j];
for (int i = 1;i < n;i++)
dp[n][i] = number[n][i];
for (int i = n;i > 1;i--) {
for (int j = 1;j <= i;j++) {
dp[i - 1][j] = max(dp[i][j], dp[i][j + 1]) + number[i - 1][j];
}
}
cout << dp[1][1] << endl;
return 0;
}
|
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式
一行,若干个整数,中间由空格隔开。
输出格式
两行,每行一个整数,第一个数字表示这套系统最多能拦截多少导弹,第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
样例 #1
样例输入 #1
1
| 389 207 155 300 299 170 158 65
|
样例输出 #1
提示
对于前 $50%$ 数据(NOIP 原题数据),满足导弹的个数不超过 $10^4$ 个。该部分数据总分共 $100$ 分。可使用$\mathcal O(n^2)$ 做法通过。
对于后 $50%$ 的数据,满足导弹的个数不超过 $10^5$ 个。该部分数据总分也为 $100$ 分。请使用 $\mathcal O(n\log n)$ 做法通过。
对于全部数据,满足导弹的高度为正整数,且不超过 $5\times 10^4$。
此外本题开启 spj,每点两问,按问给分。
$\text{upd 2022.8.24}$:新增加一组 Hack 数据。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 50;
vector<int>a, b, c;
int main() {
int n;
while (cin >> n) { a.push_back(n); }
for (int i = 0;i < a.size();i++) {
if (b.size() == 0 || a[i] <= b.back())
b.push_back(a[i]);
else {
int l = 0, r = b.size() - 1;
int pos = 0;
while (l < r) {
pos = (l + r) / 2;
if (b[pos] >= a[i])l = pos + 1;
else r = pos;
}
b[l] = a[i];
}
if (c.size() == 0 || c.back() < a[i])
c.push_back(a[i]);
else {
int l = 0, r = c.size() - 1;
int pos = 0;
while (l < r) {
pos = (l + r) / 2;
if (c[pos] < a[i])l = pos + 1;
else r = pos;
}
c[l] = a[i];
}
}
cout << b.size() << endl;
cout << c.size() << endl;
return 0;
}
|
$n$ 位同学站成一排,音乐老师要请其中的 $n-k$ 位同学出列,使得剩下的 $k$ 位同学排成合唱队形。
合唱队形是指这样的一种队形:设 $k$ 位同学从左到右依次编号为 $1,2,$ … $,k$,他们的身高分别为 $t_1,t_2,$ … $,t_k$,则他们的身高满足 $t_1< \cdots <t_i>t_{i+1}>$ … $>t_k(1\le i\le k)$。
你的任务是,已知所有 $n$ 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入格式
共二行。
第一行是一个整数 $n$($2\le n\le100$),表示同学的总数。
第二行有 $n$ 个整数,用空格分隔,第 $i$ 个整数 $t_i$($130\le t_i\le230$)是第 $i$ 位同学的身高(厘米)。
输出格式
一个整数,最少需要几位同学出列。
样例 #1
样例输入 #1
1
2
| 8
186 186 150 200 160 130 197 220
|
样例输出 #1
提示
对于 $50%$ 的数据,保证有 $n \le 20$。
对于全部的数据,保证有 $n \le 100$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| void solve() {
int n;cin >> n;
vector<int>t;
for (int i = 0; i < n; i++) {
int x;cin >> x;
t.push_back(x);
}
int k = 1;
for (int m = 0;m < n;m++) {
// 枚举中间位m
vector<int>l, r;
// 左边最长上升子序列
for (int i = 0;i < m;i++) {
if (t[i] >= t[m])continue;
if (l.size()!=0) {
if (t[i] > l.back()) {
l.push_back(t[i]);
}
else {
auto it = lower_bound(l.begin(), l.end(), t[i]);
*it = t[i];
}
}
else {
l.push_back(t[i]);
}
}
// 右边最长上升子序列
for (int i = n - 1;i > m;i--) {
if (t[i] >= t[m])continue;
if (r.size()!=0) {
if (t[i] > r.back()) {
r.push_back(t[i]);
}
else {
auto it = lower_bound(r.begin(), r.end(), t[i]);
*it = t[i];
}
}
else {
r.push_back(t[i]);
}
}
k = max(k, (int)l.size() + (int)r.size() + 1);
}
cout << n - k << endl;
}
|
题目背景
恶魔猎手尤迪安野心勃勃,他背叛了暗夜精灵,率领深藏在海底的娜迦族企图叛变。
守望者在与尤迪安的交锋中遭遇了围杀,被困在一个荒芜的大岛上。
为了杀死守望者,尤迪安开始对这个荒岛施咒,这座岛很快就会沉下去。到那时,岛上的所有人都会遇难。
守望者的跑步速度为 $17m/s$,以这样的速度是无法逃离荒岛的。庆幸的是守望者拥有闪烁法术,可在 $1s$ 内移动 $60m$,不过每次使用闪烁法术都会消耗魔法值 $10$ 点。守望者的魔法值恢复的速度为 $4$ 点每秒,只有处在原地休息状态时才能恢复。
现在已知守望者的魔法初值 $M$,他所在的初始位置与岛的出口之间的距离 $S$,岛沉没的时间 $T$。你的任务是写一个程序帮助守望者计算如何在最短的时间内逃离荒岛,若不能逃出,则输出守望者在剩下的时间内能走的最远距离。
注意:守望者跑步、闪烁或休息活动均以秒为单位,且每次活动的持续时间为整数秒。距离的单位为米。
输入格式
输入数据共一行三个非负整数,分别表示 $M$,$S$,$T$。
输出格式
输出数据共两行。
第一行一个字符串 $\texttt{Yes}$ 或 $\texttt{No}$,即守望者是否能逃离荒岛。
第二行包含一个整数。第一行为 $\texttt{Yes}$ 时表示守望者逃离荒岛的最短时间;第一行为 $\texttt{No}$ 时表示守望者能走的最远距离。
样例 #1
样例输入 #1
样例输出 #1
样例 #2
样例输入 #2
样例输出 #2
提示
对于 $30%$ 的数据,$1 \le T \le 10$,$ 1 \le S \le 100$;
对于 $50%$ 的数据,$1 \le T \le 10^3$,$ 1 \le S \le 10^4$;
对于 $100%$ 的数据,$1 \le T \le 3\times 10^5$,$0 \le M \le 10^3$,$ 1 \le S \le 10^8$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void solve() {
ll m, s, t;cin >> m >> s >> t;
vector<ll>f(t + 1);
f[0] = 0;ll bl = m;
for (ll i = 1;i <= t;i++) {
if (bl >= 10) {
f[i] = f[i - 1] + 60;
bl -= 10;
}
else {
f[i] = f[i - 1];
bl += 4;
}
}
for (int i = 1;i <= t;i++) {
f[i] = max(f[i], f[i - 1] + 17);
}
if (f[t] >= s) {
cout << "Yes\n";
cout << lower_bound(f.begin(), f.end(), s) - f.begin() << endl;
}
else {
cout << "No\n" << f[t] << endl;
}
}
|
题目背景
小明过生日的时候,爸爸送给他一副乌龟棋当作礼物。
乌龟棋的棋盘是一行 $N$ 个格子,每个格子上一个分数(非负整数)。棋盘第 $1$ 格是唯一的起点,第 $N$ 格是终点,游戏要求玩家控制一个乌龟棋子从起点出发走到终点。
乌龟棋中 $M$ 张爬行卡片,分成 $4$ 种不同的类型($M$ 张卡片中不一定包含所有 $4$ 种类型的卡片,见样例),每种类型的卡片上分别标有 $1,2,3,4$ 四个数字之一,表示使用这种卡片后,乌龟棋子将向前爬行相应的格子数。游戏中,玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片,控制乌龟棋子前进相应的格子数,每张卡片只能使用一次。
游戏中,乌龟棋子自动获得起点格子的分数,并且在后续的爬行中每到达一个格子,就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的分数总和。
很明显,用不同的爬行卡片使用顺序会使得最终游戏的得分不同,小明想要找到一种卡片使用顺序使得最终游戏得分最多。
现在,告诉你棋盘上每个格子的分数和所有的爬行卡片,你能告诉小明,他最多能得到多少分吗?
输入格式
每行中两个数之间用一个空格隔开。
第 $1$ 行 $2$ 个正整数 $N,M$,分别表示棋盘格子数和爬行卡片数。
第 $2$ 行 $N$ 个非负整数,$a_1,a_2,…,a_N$,其中 $a_i$ 表示棋盘第 $i$ 个格子上的分数。
第 $3$ 行 $M$ 个整数,$b_1,b_2,…,b_M$,表示 $M$ 张爬行卡片上的数字。
输入数据保证到达终点时刚好用光$M$张爬行卡片。
输出格式
$1$ 个整数,表示小明最多能得到的分数。
样例 #1
样例输入 #1
1
2
3
| 9 5
6 10 14 2 8 8 18 5 17
1 3 1 2 1
|
样例输出 #1
提示
每个测试点 1s。
小明使用爬行卡片顺序为 $1,1,3,1,2$,得到的分数为 $6+10+14+8+18+17=73$。注意,由于起点是 $1$,所以自动获得第 $1$ 格的分数 $6$。
对于 $30%$ 的数据有 $1≤N≤30,1≤M≤12$。
对于 $50%$ 的数据有 $1≤N≤120,1≤M≤50$,且 $4$ 种爬行卡片,每种卡片的张数不会超过 $20$。
对于 $100%$ 的数据有 $1≤N≤350,1≤M≤120$,且 $4$ 种爬行卡片,每种卡片的张数不会超过 $40$;$0≤a_i≤100,1≤i≤N,1≤b_i≤4,1≤i≤M$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| void solve() {
ll n, m;cin >> n >> m;
vector<ll>a(n + 1);
for (ll i = 1;i <= n;i++) {
cin >> a[i];
}
vector<ll>cnt(5);
for (int i = 0;i < m;i++) {
ll x;cin >> x;
cnt[x]++;
}
vector<vector<vector<vector<ll>>>>dp(cnt[1] + 1, vector<vector<vector<ll>>>(cnt[2] + 1, vector<vector<ll>>(cnt[3] + 1, vector<ll>(cnt[4] + 1, 0))));
dp[0][0][0][0] = a[1];
for (int i = 0;i <= cnt[1];i++) {
for (int j = 0;j <= cnt[2];j++) {
for (int k = 0;k <= cnt[3];k++) {
for (int l = 0;l <= cnt[4];l++) {
ll x = i * 1 + j * 2 + k * 3 + l * 4 + 1; // 走到的格子是x
if (i > 0)
// 走到x的时候,如果i > 0,那么就可以从i - 1走到i,下面同理
dp[i][j][k][l] = max(dp[i][j][k][l], dp[i - 1][j][k][l] + a[x]);
if (j > 0)
dp[i][j][k][l] = max(dp[i][j][k][l], dp[i][j - 1][k][l] + a[x]);
if (k > 0)
dp[i][j][k][l] = max(dp[i][j][k][l], dp[i][j][k - 1][l] + a[x]);
if (l > 0)
dp[i][j][k][l] = max(dp[i][j][k][l], dp[i][j][k][l - 1] + a[x]);
}
}
}
}
cout << dp[cnt[1]][cnt[2]][cnt[3]][cnt[4]] << endl;
}
|
有一条奶牛冲出了围栏,来到了一处圣地(对于奶牛来说),上面用牛语写着一段文字。
现用汉语翻译为:
有 $N$ 个区间,每个区间 $x,y$ 表示提供的 $x\sim y$ 共 $y-x+1$ 堆优质牧草。你可以选择任意区间但不能有重复的部分。
对于奶牛来说,自然是吃的越多越好,然而奶牛智商有限,现在请你帮助他。
输入格式
第一行一个整数 $N$。
接下来 $N$ 行,每行两个数 $x,y$,描述一个区间。
输出格式
输出最多能吃到的牧草堆数。
样例 #1
样例输入 #1
样例输出 #1
提示
$1 \leq n \leq 1.5 \times 10^5$,$0 \leq x \leq y \leq 3 \times 10^6$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void solve() {
ll n;cin >> n;
map<ll, vector<ll>> mp;
ll my = 0;
for (ll i = 0;i < n;i++) {
ll x, y;cin >> x >> y;
x += 1;y += 1; // 避免越界
my = max(my, y);
mp[y].push_back(x);
}
vector<ll>dp(my + 1, 0);
dp[0] = 0;
for (ll i = 1;i <= my;i++) {
dp[i] = dp[i - 1];
if (mp.count(i)) {
for (ll j = 0;j < mp[i].size();j++) {
ll y = mp[i][j];
dp[i] = max(dp[i], dp[y - 1] + i - y + 1);
}
}
}
cout << dp[my] << endl;
}
|





